Gerilime
Gerilme, uygulanan F kuvvetinin bir kesit alanına oranıdır – “birim alan başına kuvvet” olarak tanımlanır.
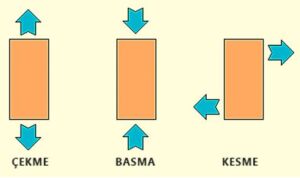
- çekme gerilimi – malzemeyi germe veya uzatma eğiliminde olan dik yönde gerilim
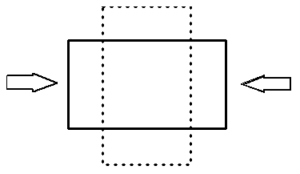
- basma gerilimi – malzemeyi sıkıştırmaya veya kısaltmaya meyilli dik yönde gerilim
- kesme gerilimi – malzemeyi kesme eğiliminde olan gerilim – basınç veya çekme gerilimine dik açılarda etkir.
Çekme veya Basma Gerilimi – Normal Gerilim
Düzlemin normal çekme veya basma gerilmesi genellikle “normal gerilme” veya “doğrudan gerilme” olarak belirtilir ve şu şekilde ifade edilebilir:
σ = Fn / A (1)
σ = normal gerilim (Pa (N/m2), psi (lbf/in2))
Fn = alana dik etki eden normal kuvvet (N, lbf)
A = alan(m2, in2)
- Birim kip (kilopound)1000 lbf (pounds-force)’ye eşittir
- 1 kip = 4448.2216 Newtons (N) = 4.4482216 kilo Newtons (kN)
Normal bir kuvvet alana dik etki eder ve dış yükler bir cismin iki bölgesini itme veya çekme eğiliminde olduğunda gelişir.
Örnek – Bir Çubuğa Etki Eden Çekme Kuvveti
10 mm çapında dairesel bir çubuğa 10 kN’luk bir kuvvet etki etmektedir. Çubuktaki gerilim(stres) şu şekilde hesaplanabilir:
σ = (10 103 N) / (π ((10 10-3 m) / 2)2)
= 127388535 (N/m2)
= 127 (MPa)
Örnek – Kare bir Kalasa Etki Eden Basma Kuvveti
120.000 N’lik bir basma yükü, 20×20 cm lik bir kalasa etki etmektedir. Kalasın sıkıştırılmış boyutu 18×18 cm’dir ve basma gerilimi (basıncı) şu şekilde hesaplanabilir:
σ = (120.000 N) / ((0,18 m) (0,18 m))
= 3703703 (N/m2)
= 3,70 (Mpa)
Kesme Gerilimi
Bir düzleme paralel gerilim genellikle “kesme gerilimi” olarak belirtilir ve şu şekilde ifade edilebilir:
τ = Fp / A (2)
τ = kesme gerilimi (Pa (N/m2), psi (lbf/in2))
Fp = alan düzleminde kesme gerilimi (N, lbf)
A = alan (m2, in2)
Bir alanın düzleminde bir kesme kuvveti bulunur ve dış yükler bir cismin iki bölgesinin birbiri üzerinde kaymasına neden olduğunda gelişir.
Gerinim (Deformasyon)
Gerinim, “gerilme nedeniyle bir katının deformasyonu” olarak tanımlanır.
- Normal gerilme – bir çizgi parçasının uzaması veya daralması
- Kesme gerilimi – başlangıçta dik olan iki çizgi parçası arasındaki açıda değişiklik
Normal gerilme ve şu şekilde ifade edilebilir:
ε = dl / lo
= σ / E (3)
dl = uzunluktaki değişim (m, in)
lo = ilk uzunluk (m, in)
ε = gerinim – birimsizdir!
E = Young’s modülü (Elastisite Modülü) (Pa , (N/m2), psi (lbf/in2))
Young modülü, bir kuvvete maruz kaldığında bir nesnenin uzamasını veya sıkışmasını tahmin etmek için kullanılabilir.
Gerinim, iki uzunluğun oranı olduğu için boyutsuz bir birimdir. Ancak bunu iki uzunluk biriminin oranı olarak ifade etmek de yaygın bir uygulamadır – m/m veya in/in gibi.
Bazı malzemelerin Young’s modülü değerleri
| Young’s Modülü Elastisite – E – (106 psi) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Metal | Sıcaklık (oC) | ||||||||||||||
| -200 | -129 | -73 | 21 | 93 | 149 | 204 | 260 | 316 | 371 | 427 | 482 | 538 | 593 | 649 | |
| Sıcaklık (oF) | |||||||||||||||
| -325 | -200 | -100 | 70 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 | |
| Dökme demir | |||||||||||||||
| Gri dökme demir | 13.4 | 13.2 | 12.9 | 12.6 | 12.2 | 11.7 | 11.0 | 10.2 | |||||||
| Çelik | |||||||||||||||
| Karbon çeliği C <= 0.3% | 31.4 | 30.8 | 30.2 | 29.5 | 28.8 | 28.3 | 27.7 | 27.3 | 26.7 | 25.5 | 24.2 | 22.4 | 20.4 | 18.0 | |
| Karbon çeliği C => 0.3% | 31.2 | 30.6 | 30.0 | 29.3 | 28.6 | 28.1 | 27.5 | 27.1 | 26.5 | 25.3 | 24.0 | 22.2 | 20.2 | 17.9 | 15.4 |
| Nikel çeliği Ni 2% – 9% | 29.6 | 29.1 | 28.5 | 27.8 | 27.1 | 26.7 | 26.1 | 25.7 | 25.2 | 24.6 | 23.0 | ||||
| Cr-Mo çeliği Cr 1/2% – 2% | 31.6 | 31.0 | 30.4 | 29.7 | 29.0 | 28.5 | 27.9 | 27.5 | 26.9 | 26.3 | 25.5 | 24.8 | 23.9 | 23.0 | 21.8 |
| Cr-Mo çeliği Cr 2 1/4% – 3% | 32.6 | 32.0 | 31.4 | 30.6 | 29.8 | 29.4 | 28.8 | 28.3 | 27.7 | 27.1 | 26.3 | 25.6 | 24.6 | 23.7 | 22.5 |
| Cr-Mo çeliği Cr 5% – 9% | 32.9 | 32.3 | 31.7 | 30.9 | 30.1 | 29.7 | 29.0 | 28.6 | 28.0 | 27.3 | 26.1 | 24.7 | 22.7 | 20.4 | 18.2 |
| krominyum çeliği Cr 12%, 17%, 27% | 31.2 | 30.7 | 30.1 | 29.2 | 28.5 | 27.9 | 27.3 | 26.7 | 26.1 | 25.6 | 24.7 | 23.2 | 21.5 | 19.1 | 16.6 |
| Ostenetik çelik (TP304, 310, 316, 321, 347) | 30.3 | 29.7 | 29.1 | 28.3 | 27.6 | 27.0 | 26.5 | 25.8 | 25.3 | 24.8 | 24.1 | 23.5 | 22.8 | 22.1 | 21.2 |
| Bakır ve bakır alaşımları | |||||||||||||||
| Comp. and leaded-Sn bronz (C83600, C92200) | 14.8 | 14.6 | 14.4 | 14.0 | 13.7 | 13.4 | 13.2 | 12.9 | 12.5 | 12.0 | |||||
| Gemi pirinci Si & Al bronz (C46400, C65500, C95200, C95400) | 15.9 | 15.6 | 15.4 | 15.0 | 14.6 | 14.4 | 14.1 | 13.8 | 13.4 | 12.8 | |||||
| Bakır (C11000) | 16.9 | 16.6 | 16.5 | 16.0 | 15.6 | 15.4 | 15.0 | 14.7 | 14.2 | 13.7 | |||||
| bakır kırmızı pirinç Al-bronz (C10200, C12000, C12200, C12500, C14200, C23000, C61400) | 18.0 | 17.7 | 17.5 | 17.0 | 16.6 | 16.3 | 16.0 | 15.6 | 15.1 | 14.5 | |||||
| Nikel ve nikel alaşımları | |||||||||||||||
| Monel 400 (N04400) | 27.8 | 27.3 | 26.8 | 26.0 | 25.4 | 25.0 | 24.7 | 24.3 | 24.1 | 23.7 | 23.1 | 22.6 | 22.1 | 21.7 | 21.2 |
| Titanyum | |||||||||||||||
| Alaşımsız titanyum 1, 2, 3 ve 7 | 15.5 | 15.0 | 14.6 | 14.0 | 13.3 | 12.6 | 11.9 | 11.2 | |||||||
| Aluminyum ve aluminyum alaşımları | |||||||||||||||
| Dereceler 443, 1060, 1100, 3003, 3004, 6063 | 11.1 | 10.8 | 10.5 | 10.0 | 9.6 | 9.2 | 8.7 | ||||||||
Poisson oranı, bağıl kasılma (büzülme) geriniminin oranıdır.
Poisson’s oranı aşağıdaki gibi tanımlanabilir.
μ = – εt / εl
μ = Poisson’s oranı
εt = Enine gerinim (m/m, ft/ft)
εl = boyuna veya eksenel gerinim (m/m, ft/ft)
Bazı malzemelerin Possion’s oranları
|
Materyal
|
Poisson’s oranı
– μ – |
|---|---|
| Üst Limit | 0.5 |
| Aluminyum | 0.334 |
| Aluminyum, 6061-T6 | 0.35 |
| Aluminyum, 2024-T4 | 0.32 |
| Berilyum bakır | 0.285 |
| Pirinç, 70-30 | 0.331 |
| Pirinç, döküm | 0.357 |
| Bronz | 0.34 |
| Kil | 0.41 |
| Beton | 0.1 – 0.2 |
| Bakır | 0.355 |
| Paslanmaz Çelik | 18-80.305 |
| Demir, Döküm | 0.22 – 0.30 |
| Çelik, Döküm | 0.265 |
| Titanyum (99.0 Ti) | 0.32 |
Örnek – Gerilme ve Uzunluk Değişimi
Yukarıdaki örnekteki çubuk 2 m uzunluğundadır ve Elastisite Modülü 200 GPa (200 109 N/m2) olan çelikten yapılmıştır. Uzunluk değişimi (3)’ün şuna dönüştürülmesiyle hesaplanabilir:
dl = σ lo / E
= (127 106 Pa) (2 m) / (200 109 Pa)
= 0.00127 m
= 1.27 mm
Gerinim Enerjisi
Bir nesne gerildiğinde, içinde enerji depolar. Eksenel bir yük için depolanan enerji şu şekilde ifade edilebilir:
U = 1/2 Fn dl
U = deformasyon enerjisi (J (N m), ft lb)
Young Modülü – Elastisite Modülü (veya Çekme Modülü) – Hooke Yasası
Çoğu metal, üzerine uygulanan yükle orantılı olarak deforme olur. Hooke Yasası ile ifade edildiği gibi, gerilme yük ile orantılıdır ve gerinim deformasyon ile orantılıdır.
E = gerilim / gerinim (stress / strain)
= σ / ε
= (Fn / A) / (dl / lo) (4)
E = Young’s Modulü (N/m2) (lb/in2, psi)
Elastisite Modülü veya Young Modülü, yaygın olarak metaller ve metal alaşımları için kullanılır ve 106 lbf/in2, N/m2 veya Pa olarak ifade edilir. Çekme modülü genellikle plastikler için kullanılır ve 105 lbf/in2 veya GPa. olarak ifade edilir.
Kesme Elastisite Modülü – veya Rijidite Modülü
G = gerilim / gerinim (stress / strain)
= τ / γ
= (Fp / A) / (s / d) (5)
G = Kesme elastisite modülü veya rijidite modülü (N/m2) (lb/in2, psi)
τ = kesme gerilmesi ((Pa) N/m2, psi)
γ = birimsiz kesme gerilmesi ölçüsü
Fp =hareket ettikleri yüzlere paralel kuvvet
A = alan (m2, in2)
s = yüzlerin yerdeğiştirme miktarı (m, in)
d = hareket eden yüzler arasındaki mesafe (m, in)
Esneklik Kitle Katsayısı (Bulk Modulus Elasticity)
Esneklik kitle katsayısı- veya Hacim Modülü – maddenin düzgün sıkıştırmaya karşı direncinin bir ölçüsüdür. Esneklik kitle katsayısı, eksenel yüklemeye maruz kalan bir malzemenin hacmindeki değişime gerilme oranıdır.
| Materyal | Young’s Modulü – E – |
Kesme Modulü – G – |
Esneklik Modülü – K – |
|---|---|---|---|
| (GPa) (106 psi) |
(GPa) (106 psi) |
(GPa) (106 psi) |
|
| Aluminyum | 70 | 24 | 70 |
| Pirinç | 91 | 36 | 61 |
| Bakır | 110 | 42 | 140 |
| Cam | 55 | 23 | 37 |
| Demir | 91 | 70 | 100 |
| Kurşun | 16 | 5.6 | 7.7 |
| çelik | 200 | 84 | 160 |
- 1 GPa = 109 Pa (N/m2)
- 106 psi = 1 Mpsi = 103 ksi